In Euclidean Geometry, a special kind of ellipse which has an eccentricity that equals zero and the two foci coincidence is called a circle. A circle can also be defined by saying that it is the figure that is traced when a locus of points are drawn at an equidistant from the center. There are many topics that students need to learn such as properties, circumference, area of circle, etc. Before we talk about the concepts associated with a circle we have to first understand the terms associated with it.
Different Parts of a Circle
- Arc – A connected portion on the circumference of the circle is known as an arc
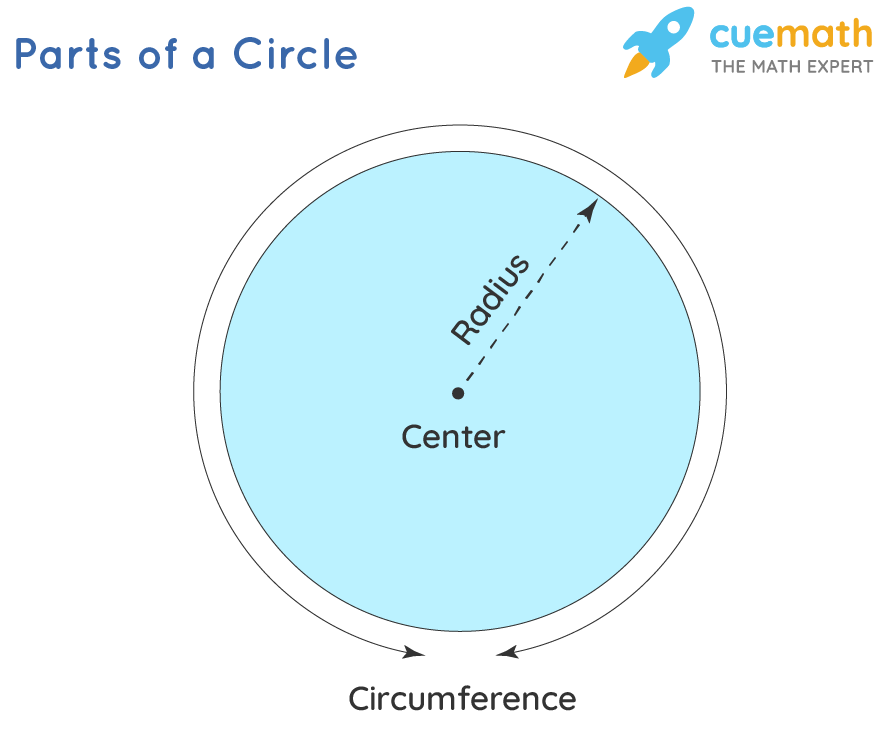
- Centre – It is a point within the circle that is at the same distance from all points lying on the circumference of the circle.
- Chord – A line segment whose endpoints are on the circle is known as a chord.
- Diameter – The longest chord of the circle that passes through the centre is called the diameter. The circle contains the endpoints of a diameter.
- Radius – A radius is half the diameter of a circle and the end points of this line segment lies on the circumference.
- Segment – The region formed between a chord and an arc is known as a segment. A point to note is that the segment never contains the center of the circle.
- Sector – The region between either of the two arcs and any two radii is called a sector.
- Semi Circle – One definition of a semicircle is the region that is bound between the diameter and one of the two arcs. It is exactly half of the circle.
- Tangent – A tangent is that line that can extend infinitely and touches a circle exactly at one single point. If there are two tangents and they touch the diameter at its end points then these two lines will always be parallel.
Area of a Circle
We can define the area of a circle to be the entire region or space that is encompassed by the boundary of the figure. If we have the radius or diameter of a circle, then we can easily apply the given formula to find the area:
Area of a circle = pi * r2, where pi is a constant that equals 3.14 or 22/7 and r is the radius
Area = pi * (d / 2)2, As the diameter is equal to half of the measurement of the radius we can express the area as given above.
Circumference of a Circle
The circle’s circumference is similar to the perimeter of a polygon. It can be defined as the complete boundary of the circle. The following formula can be used to calculate the circumference of a circle.
Circumference = 2 * pi * r = pi * d
For instance, what is the area and circumference of a circle with a radius of 7cm?
Solution: Radius = 7 cm
By formulas:
- Circumference = 2 * pi * r = 2 * (22/7) * 7 = 44 cm
- Area = pi * r2 = (22/7) * (7)2 = 154 cm2
Conclusion
There are several geometrical and analytical conclusions that can be drawn from a circle. A child always requires proper guidance to reach reasonable conclusions. Cuemath is the perfect place to do this. It is an online educational platform that helps kids build a strong and robust mathematical foundation. The math experts are certified and use several comprehensive resources such as workbooks, math worksheets, interactive games and so on. Thus, a child is in very reliable and knowledgeable hands at Cuemath. To learn more visit cuemath.com.